 jest zbiorem zwartym w
jest zbiorem zwartym w  oraz
oraz
 jest funkcją ciągłą,to
jest funkcją ciągłą,to
 jest zbiorem zwartym w
jest zbiorem zwartym w 
Twierdzenie Weierstrassa
Okazuje się, że jeśli weźmiemy obraz przez funkcję ciągłą zbioru zwartego, to otrzymamy także zbiór zwarty.
Twierdzenie I
Jeśli
 jest zbiorem zwartym w
jest zbiorem zwartym w  oraz
oraz
 jest funkcją ciągłą,to
jest funkcją ciągłą,to
 jest zbiorem zwartym w
jest zbiorem zwartym w 
Dowód
Aby pokazać zwartość zbioru  weźmy dowolny ciąg
weźmy dowolny ciąg  Ponieważ każde
Ponieważ każde  jest w obrazie zbioru
jest w obrazie zbioru  ,więc
dla każdego
,więc
dla każdego  istnieje
istnieje  takie, że
takie, że
 Ponieważ zbiór
Ponieważ zbiór  jest zwarty(z założenia), zatem dla
ciągu
jest zwarty(z założenia), zatem dla
ciągu  istnieje podciąg
istnieje podciąg  zbieżny w
zbieżny w  to znaczy
to znaczy
Z ciągłości funkcji  wynika, że
wynika, że

zatem pokazaliśmy, że ciąg  posiada podciąg zbieżny w
posiada podciąg zbieżny w  co kończy dowód zwartości
co kończy dowód zwartości 
Twierdzenie II(Weierstrassa)
Jeśli  jest zbiorem zwartym oraz
jest zbiorem zwartym oraz  jest funkcją ciągłą,
to funkcja
jest funkcją ciągłą,
to funkcja  osiąga swoje kresy, to znaczy
osiąga swoje kresy, to znaczy

Dowód
Ponieważ funkcja  jest ciągła, a zbiór
jest ciągła, a zbiór  jest zwarty, więc z twierdzenia I wynika, że
zbiór
jest zwarty, więc z twierdzenia I wynika, że
zbiór  jest zwarty, a zatem także ograniczony, to znaczy
jest zwarty, a zatem także ograniczony, to znaczy
Należy pokazać, że
Pokażemy istnienie  o powyższej własności(dowód istnienia
o powyższej własności(dowód istnienia  jest analogiczny).
jest analogiczny).
Niech  oraz dla dowodu niewprost, przypuśćmy, że
oraz dla dowodu niewprost, przypuśćmy, że  nie jest realizowane, to znaczy
nie jest realizowane, to znaczy
Zdefiniujmy nową funkcję  w następujący sposób:
w następujący sposób:
Definicja  jest poprawna (gdyż mianownik jest niezerowy) oraz funkcja
jest poprawna (gdyż mianownik jest niezerowy) oraz funkcja  jest ciągła.
Korzystając ponownie z twierdzenia I wiemy, że zbiór
jest ciągła.
Korzystając ponownie z twierdzenia I wiemy, że zbiór  jest zwarty, a zatem także ograniczony,
zatem jego supremum
jest zwarty, a zatem także ograniczony,
zatem jego supremum  jest skończone, czyli
jest skończone, czyli

Oczywiście

Dla dowolnego  mamy
mamy
w szczególności  sprzeczność.
sprzeczność.
Wykazaliśmy zatem, że funkcja  osiąga swój kres dolny, czyli
osiąga swój kres dolny, czyli

Uwaga
Założenie zwartości w twierdzeniu Weierstrassa jest niezbędne.
Rozważmy funkcję  daną wzorem
daną wzorem  Jest ona ciągła,
Jest ona ciągła,

ale dla żadnego punktu  funkcja
funkcja  nie przyjmuje
wartości
nie przyjmuje
wartości  i
i 
Założenia twierdzenia Weierstrassa nie są tutaj spełnione gdyż
zbiór  nie jest zwarty.
nie jest zwarty.
Twierdzenie Darboux
Wykażemy teraz użyteczny lemat mówiący, że jeśli funkcja ciągła jest dodatnia w pewnym punkcie, to jest także dodatnia w pewnym otoczeniu tego punktu.
Twierdzenie I
Jeśli  oraz funkcja
oraz funkcja  jest ciągła w punkcie
jest ciągła w punkcie  , to:
, to:
(1) jeśli  to
to
(2) jeśli  to
to

Dowód
(1)
Załóżmy, że funkcja  jest ciągła w punkcie
jest ciągła w punkcie  oraz
oraz
 Niech
Niech  Korzystając z definicji Cauchy'ego granicy funkcji w punkcie mamy, że
Korzystając z definicji Cauchy'ego granicy funkcji w punkcie mamy, że


Zatem  dla
dla 
(2) Dowód jest analogiczny.
Kolejne twierdzenie to tak zwana własność Darboux dla funkcji ciągłych.
Mówi ono, że funkcja ciągła na przedziale  i taka, że
i taka, że  i
i  posiada pierwiastek
w przedziale
posiada pierwiastek
w przedziale .bmp) Na tej własności opiera się,
stosowana w metodach numerycznych, metoda bisekcji poszukiwania miejsc zerowych funkcji.
Na tej własności opiera się,
stosowana w metodach numerycznych, metoda bisekcji poszukiwania miejsc zerowych funkcji.
Twierdzenie II(Darboux)
Jeśli  jest funkcją ciągłą,
jest funkcją ciągłą,  to
to
fc0.bmp)

Dowód
Z warunku  wynika, że funkcja
wynika, że funkcja  przyjmuje na
końcach wartości różnych znaków, tzn.
przyjmuje na
końcach wartości różnych znaków, tzn.  lub
lub  Niech na przykład
Niech na przykład  Niech
Niech  Zauważmy, że gdyby
Zauważmy, że gdyby
 to istniałoby pewne
to istniałoby pewne  takie, że dla wszystkich
takie, że dla wszystkich
 mielibyśmy
mielibyśmy  (co wynika z twierdzenia I). A zatem
(co wynika z twierdzenia I). A zatem  nie byłoby supremum
nie byłoby supremum  bo do tego zbioru należałby punkt
bo do tego zbioru należałby punkt  Analogicznie, gdyby
Analogicznie, gdyby
 to także dla
to także dla  w pewnym przedziale
w pewnym przedziale  mielibyśmy
mielibyśmy
 a zatem
a zatem  nie byłoby supremum
nie byłoby supremum  bo na
przykład punkt
bo na
przykład punkt  byłby mniejszym od
byłby mniejszym od  ograniczeniem górnym tego zbioru.
A zatem jedyna możliwość to
ograniczeniem górnym tego zbioru.
A zatem jedyna możliwość to 
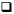
Wniosek
Jeśli  jest funkcją ciągłą,
jest funkcją ciągłą,  (odpowiednio
(odpowiednio  ),to
),to


Powyższe wyrażenia nazywamy własnością Darboux funkcji  .
.