Ciągłość funkcji

Funkcję f: D ® R nazywamy ciągłą w punkcie x0 Î D wtedy i tylko wtedy, gdy istnieje granica
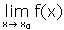i
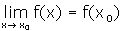czyli 1. funkcja f ma w punkcie x0 granicę g
2. granica g jest równa wartości funkcji w punkcie x0 tzn f(x0)
Funkcję f: D ® R nazywamy prawostronnie ciągłą w punkcie x0 Î D wtedy i tylko wtedy, gdy istnieje granica
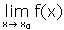i
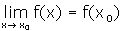Funkcję f: D ® R nazywamy lewostronnie ciągłą w punkcie xoÎ D wtedy i tylko wtedy, gdy istnieje granica
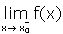i
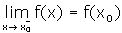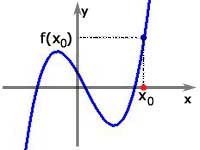
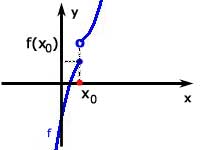
Funkcja f nie ma granicy w punkcie x0, więc nie jest ciągła w punkcie x0. Funkcja f ma granicę w punkcie x0,
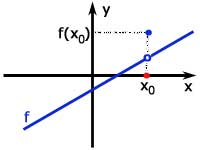
ale nie jest ciągła w punkcie x0.		 Funkcja f jest ciągła w punkcie x0

Ciągłość funkcji y=f(x) dla x0 ÎD badamy
1.obliczając f(x0) i
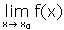2. sprawdzając, czy 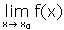= f(x0)
albo
1.obliczając 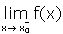i
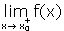2. sprawdzając, czy 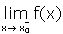= 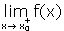= f( x0)

Mówimy, że funkcja jest ciągła, jeżeli jest ciągła w każdym punkcie swojej dziedziny, przy czym, jeśli dziedziną funkcji jest przedział jednostronnie lub obustronnie domknięty, to ciągłość funkcji w każdym należącym do niego końcu rozumiemy jako odpowiednią ciągłość jednostronną

Mówimy, że funkcja jest ciągła w przedziale (a; b), jeżeli jest ciągła w przedziale (a; b) oraz jest prawostronnie ciągła w punkcie a i lewostronnie ciągła w punkcie b.